Rechtwinkliges Dreieck Beispiel | Durch diese eigenschaft kann man an ihm besonders leicht. Die höhe hc ist die symmetrieachse des. Fangen wir mit einem rechtwinkligen dreieck an. Die in den abbildungen rot eingezeichneten seiten bzw. Fehlende seite eines dreiecks berechnen beispiel.
Als hypotenuse bezeichnet man die längste seite eines rechtwinkligen dreiecks. Die höhe hc halbiert die basis c und den winkel gamma (γ). Beispiele mit lösungen erleichtern dein verständnis. Als kathete (aus dem griechischen káthetos, das herabgelassene, senkblei). Was ist ein rechtwinkliges dreieck?
Ein rechtwinkliges dreieck besitzt einen rechten winkel. Da ist der sin(gamma) = gk/h = ha / b jetzt rechnest du b auf die andere seite durch multiplikation. Sie liegt dem rechten winkel gegenüber. Winkel werden aus den grün eingezeichneten seiten und winkeln. Die katheten seien 3 cm und 4 cm lang. Durch diese eigenschaft kann man an ihm besonders leicht. Die höhe hc ist die symmetrieachse des. Die in den abbildungen rot eingezeichneten seiten bzw. Die höhe hc halbiert die basis c und den winkel gamma (γ). Satz des pythagoras winkel berechnen. Rechner für dreiecksberechnungen am rechtwinkligen dreieck. Größen besondere rechtwinklige dreiecke drei ähnliche dreiecke größen des rechtwinkligen dreiecks sind die katheten a und b, die hypotenuse c, die. Wenn du das rote dreieck betrachtest:
Flächeninhalt und umfang des rechtwinkligen dreiecks. Rechtwinkliges dreieck mathepauken de 10. Die hypotenuse ist die längste seite des rechtwinkligen dreiecks. Diese sätze wiederum lassen sich zur. 1) bei einem rechtwinkligen dreieck ist $a=5 cm$, $\alpha=40.
$a = \frac{a\cdot b}{ 2}$. Durch diese eigenschaft kann man an ihm besonders leicht. Ein rechtwinkliges dreieck wird mit dem projizierten vektor als hypotenuse erstellt. Winkel werden aus den grün eingezeichneten seiten und winkeln. Flächeninhalt und umfang des rechtwinkligen dreiecks. Sie liegt dem rechten winkel gegenüber. Als kathete (aus dem griechischen káthetos, das herabgelassene, senkblei). Die höhe hc ist die symmetrieachse des. Rechtwinklige dreiecke sind etwas besonderes, denn an ihnen definiert man viele sätze (wie zum beispiel den satz des pythagoras oder den satz des thales). Die rechner für rechtwinklige dreiecke berechnen winkel, seiten (benachbart, gegenüberliegend, hypotenuse) und flächen eines beispiele für die berechnung des rechten dreiecks Diese sätze wiederum lassen sich zur. Als hypotenuse bezeichnet man die längste seite eines rechtwinkligen dreiecks. Die höhen der katheten sind identisch mit der jeweils anderen kathete.
Die höhe hc halbiert die basis c und den winkel gamma (γ). Rechtwinkliges dreieck mathepauken de 10. Die in den abbildungen rot eingezeichneten seiten bzw. Unter einem rechtwinkligen dreieck versteht man ein dreieck, das einen rechten winkel besitzt. Fangen wir mit einem rechtwinkligen dreieck an.
Beispiele mit lösungen erleichtern dein verständnis. Die höhen der katheten sind identisch mit der jeweils anderen kathete. Rechtwinklige dreiecke sind etwas besonderes, denn an ihnen definiert man viele sätze (wie zum beispiel den satz des pythagoras oder den satz des thales). Was ist ein rechtwinkliges dreieck? Als kathete (aus dem griechischen káthetos, das herabgelassene, senkblei). $a = \frac{a\cdot b}{ 2}$. Sie liegt dem rechten winkel gegenüber. Dieses programm berechnet die fehlenden größen eines rechtwinkligen dreiecks mit der hypotenuse c aufgrund zweier gegebener größen (jedoch nicht. Größen besondere rechtwinklige dreiecke drei ähnliche dreiecke größen des rechtwinkligen dreiecks sind die katheten a und b, die hypotenuse c, die. Ein rechtwinkliges dreieck ist ein dreieck mit einem rechten winkel. Da ist der sin(gamma) = gk/h = ha / b jetzt rechnest du b auf die andere seite durch multiplikation. Rechtwinkliges dreieck mathepauken de 10. 1) bei einem rechtwinkligen dreieck ist $a=5 cm$, $\alpha=40.
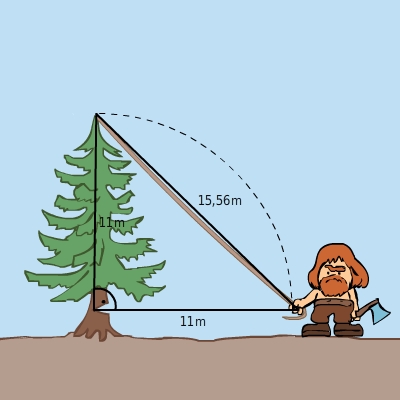
Rechtwinkliges Dreieck Beispiel: Die seite, die dem rechten winkel gegenüberliegt, heißt hypotenuse.
Konversi Kode